astroinformatics.de

 

Its been a while ago I started this series about measuring photo events with modern digital cameras used in astronomy. In my previous articles I provided a sketch of the light detection process in a modern CMOS camera, that is described by quantum efficiency qν and camera gain gPC. Also we shed light on camera gain gPC, that is the unity gain condition and discussed this situation with a typical DSLR camera. This monthly notice will focus on the Vega photometric system.

 

Photometric systems 

There are currently three major photometric systems in astronomy:

  • ABν magnitude system
  • STλ magnitude system
  • Vega system, also referred as Johnson photometric system 

 

The ABν magnitudes system (ABMag) is defined as a monochromatic flux constant in frequency, while the STλ magnitude system is defined as a monochromatic flux constant in wavelength. Both, the ABν and STλ systems, are artificial photometric systems defining different zeropoints for existing photometric filter systems. The Vega system or Johnson system historically is based on experimental measures, uses spectral flux density of real stars. Recent literature uses Vega as a prototype star and spectroscopic model to derive photometric calibration of photometric systems for any combination of filter system and detector, including the Johnson UBVRI system and Bessell's contributions to create a standard on this using different combinations and detectors that are closest to Johnsons original work. So, Vega is somehow connected to the Johnson UBV(RI) filter system. We will discuss the details about Vega later. However, don't confuse photometric systems with filter systems!

 

Apparent magnitude

The concept of apparent magnitude is the logarithm of the ratio of brightnesses of astronomical objects following Pogson's law. The difference in magnitude between two stars with fluxes ("brightness") f1 and f2 is given by:

mag = 2.5 log10 ( f1 / f2 )

A ratio of brightness will become a difference in magnitude. Two stars having fluxes (brightness) f1 and f2 with flux f2 dimmed by a factor of 100 compared to f1 the logarithm converts brightness factor into a magnitude difference of 5 mag. A difference of one mag between will yield a brightness ratio of approximately 2.512.

Throughout this article series, we follow general recommendations of journals and use the unit mag for magnitudes. If magnitudes refer to filter bands, this is indicated by letters in italic, like U, B, V, R or I in case of the Johnson-Cousins filter bands, for example. For narrow band filters it is sometimes practice to use the wavelength in nm or Angstrom, like mag5007 indicating magnitudes for an O-III narrowband filter centered at 500.7 nm. If no filter band is provided, assume to have visual apparent magnitudes, that are similar but not exactly the same, as the Johnson V band magnitude. While you may sometimes find the unit m instead of mag in astronomical literature, astronomical journals do not recommend the practice to use superscript m as the unit of magnitude.

Computations in mag are easier, the numbers more handy. Apparent magnitudes, i.e. the brightness the stars appear in the night sky, are of interest, as we want to describe the relationship between stellar magnitudes and fluxes measured. Don't confuse apparent magnitude with absolute magnitude, that is brightness as if the measurerd star would appear at a normalized distance of 10 parsec (for stars). If star f1 has apparent magnitude of 8.3 mag, then star f2 dimmed by a factor 100 in brightness will have magnitude 8.5+5=13.3 mag.

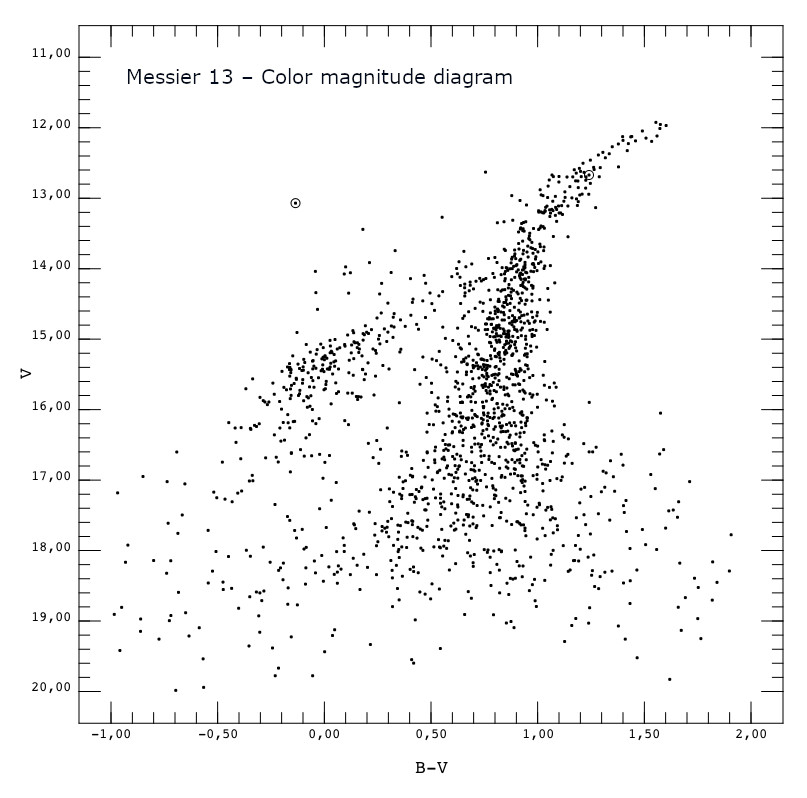
In stellar photometry the color index, or simply the color, is the difference of two magnitudes measured in different passband color filters, like the Johnson B and V filter. Colors, like B-V are used as an indicator of spectral type and finally the type of a star, from its position in a plotted color-magnitude diagram (CMD). Colors of stars are important to derive astrophysical parameters, like stellar evolution, ages or total mass of a star cluster from a CMD.

 

     

Color-magnitude diagram B-V versus V derived from high-resolution imaging of Messier 13, taken with a 8" telescope and Canon DSLR. Note the increasing magnitude errors towards faint stars at detection level around V=19. An error of 1.0 mag reflects an uncertainty of a factor 2.5 in flux (brightness). This statistical error results from of having counted few photon events, that is (intrinsic) naturals photon noise.

 

The digital range of pixel intensities recorded by a DSLR spans 14 bit, or 16 bit with dedicated astronomical cameras. So the maximum span of mag from pixel intensities, that can be measured from a single exposure at 16 bit is limited to:

Δm = 2.5 log10 ( 65536 ) ≈ 12 mag.

A magnitude range of 12 mag sounds a lot. In fact, it does not reflect the possible large intensity range of stars in a star cluster or faint nebula feature. When trying to conduct precise photometry on stellar clusters down to the faint dwarfs, 12 mag is not enough to be covered by a single exposure. Depending on the flux of the bright night sky, camera bias, actual camera gain settings, and seeing effects mag range is more limited in practice. Keep in mind, when recording with high camera gain setting this will quickly reduce magnitude range in the digital image by cutting flux from brighter stars in the image. This is why it is not recommended to use high gain or ISO settings for advanced astrophotography.

 

Vega and the zeropoint of apparent magnitudes

Magnitudes express a ratio of fluxes (brightnesses) at logarithmic scale. Fortunately, apparent magnitudes got a zero point. Vega is the brightest star in the Northern hemisphere and is of spectral type A0V. Historically, Vega defined the zero-point of apparent magnitude. A problem occurred with stellar spectral photometry, or simply the different colors of stars, when stellar evolution became a topic of interest. By definition a star of spectral type A0, like Vega, shall define the zero-point of apparent magnitude V=0.00, and also colors B-V=0.00 and U-B=0.00 in Johnson UBV (Johnson & Morgan, 1953). Measured fluxes and thus apparent magnitudes in the different passbands depend on the color filter and detector used. In the original work of Johnson & Morgan (1953) apparent magnitude and color indexes of Vega were provided as V=0.03, B-V=0.00 and U-B=0.01. The paradoxical difference between zero-point definition and actual values measured result from different filter bands, detectors and error range between observations. Also Vega is not considered a single reference star, but multiple stars will be used to calibrate photometric systems. It was Bessel (1979, 1990 and 2005), who later reported his efforts to create filter-detector combinations to deliver reproducible measures closest to Johnsons original values. His reports on the influence of filter transmission and detector susceptibility on spectral calibration influenced later calibration techniques including space telescopes. Early measures were taken using a specific 1P21 photomultiplier tube. Silicon detectors, like CCD or CMOS imaging sensors, were later covered by the attempt to run spectral calibration.

The magnitude of Vega has been reviewed and discussed many times for several reasons. Johnson & Morgan (1953) reported apparent magnitude of Vega as V=0.03. So, Vega is not a real zero point, but depends on the photometric filter system used. Slight variability of brightness is another issue with Vega. Its variability is considered to be driven by dust clouds and oscillations of Vega. Vega was also found to have high infrared excess. There are a number of reference star catalogs for calibration and also white dwarfs have been considered for calibration. Although replaced by the AB magnitude system in modern, sensitive, CCD-based astronomy due to Vega's infrared excess, Vega remains a fundamental, historical calibration reference. 

 

Conclusion and outlook

Magnitudes are connected to fluxes by Pogson's law. Apparent magnitude is a measure of brightness (flux) expressed at logarithmic scale. To summarize, Vega's apparent magnitude and colors in Johnson UBV passband filters is not exactly zero and differs when measured with different filters and detectors. Magnitude in the Johnson V passband measured with photomultiplier tubes and early filter assembly shall be assumed as V=0.03, which is a deviation of 2.8% (percent) from zero. Keep in mind, that Johnson V is not the same visual apparent magnitude as the human eye might "see" Vega.

Of more importance is: The fundamental property of the concept of apparent magnitude, its zeropoint offers the opportunity to derive apparent magnitude from photon count measures. The zeropoint defines a reference brightness used to compare apparent magnitude to the reference from where we may build the relationship between apparent magnitude and photon count. The reference could be approximately Vega and many other well known reference stars suited to derive magnitudes. For more details, see the work of Johnson & Morgan (1953), Bessel (2005) or Stritzinger (2005).

For further discussions we may ignore the minor differences of values discussed between different authors and also Vega's variability. Vega certainly must be regarded as one of many zeropoint reference stars for calibration. The Vega system is still of importance in spectrophotometry, also because spectral fluxes in different passbands may use Vega spectrum for flux calibration in various filter bands. This is also because Vega is bright to provide a good signal. This will be covered by the next article.

Stay tuned! To be continued soon...

 

Literature